Perspective Projection

Perspective projection projects objects on a plane. It has the effect that distant objects are smaller.

projection

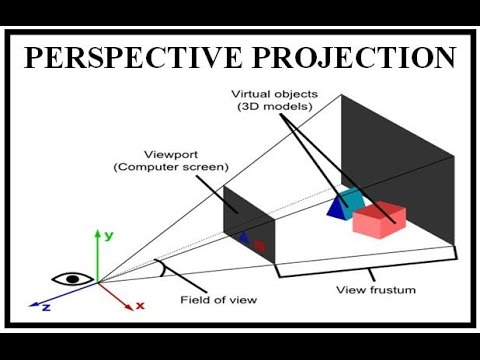
If we look at this scene in the negative x axis direction.

projection

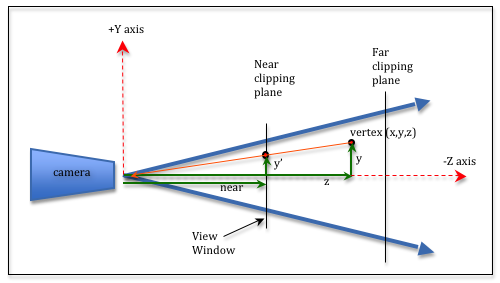
Perspective matrix is being used to transform all verteices to the near clipping plane. For example, the picture above has a vertex(x, y, z). After the perspective matrix is applied, we will get projected vertex(x’, y’, z’). The coordinates of projected vertex can be calculated based on similar triangles.

$\frac{y'}{y} = \frac{near}{-z}$

z is inversely propotional to y since near is always positive and z is negative(camera is looking at negative z direction).

$y' = \frac{near\cdot y}{-z}$

Same idea can also be applied to x’

$x' = \frac{near\cdot x}{-z}$

However, it’s impossible to construct a 3 by 3 matrix that can transforms x component in vector (x, y, z) into near multiply x divided by z.

Homogeneous Coordinates

In homogeneous coordinates, a new component w is appended. And any non zero scaler multiply with the point represent the same point.

$\begin{bmatrix} x\\ y\\ z\\ w\\\end{bmatrix}= \begin{bmatrix} \frac{1}{w}x\\ \frac{1}{w}y\\ \frac{1}{w}z\\ 1\\\end{bmatrix} = \begin{bmatrix} 2x\\ 2y\\ 2z\\ 2w\\\end{bmatrix}$

If we assume the viewing plane is at w = 1. Then all points represented by homogeneous coordinates can be divided by w in order to get the projected point on the viewing screen. In other word, if perspective matrix can output a vector that w = z. Then projected vector position can be retrieved by dividing w after perspective matrix is applied.

After applying perspective matrix:

$\begin{bmatrix} nx\\ ny\\ z\\ -z\\\end{bmatrix}$

After dividing by w component:

$\begin{bmatrix} \frac{nx}{-z}\\ \frac{ny}{-z}\\ -1\\ 1\\\end{bmatrix}$

Therefore, the perspective matrix:

$\begin{bmatrix} n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& 1& 0\\ 0& 0& -1& 0\\\end{bmatrix}$

Homogeneous Division:

$\begin{bmatrix} \frac{nx}{z}\\ \frac{ny}{z}\\ 1\\ 1\\\end{bmatrix}=\begin{bmatrix} nx\\ ny\\ z\\ z\\\end{bmatrix}=\begin{bmatrix} n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& 1& 0\\ 0& 0& -1& 0\\\end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1\\\end{bmatrix}$

Perspective Matrix

The problem of this matrix is the lost of depth information during homogeneous division(since w = -z).
If I want to keep depth information, it will be great if z component is -z^2 before homogeneous division.

$\begin{bmatrix} nx\\ ny\\ z^2\\ z\\\end{bmatrix}=\begin{bmatrix} n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& m_{1}& m_{2}\\ 0& 0& 1& 0\\\end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1\\\end{bmatrix}$

That gives us:

$zm_{1}+m_{2}=z^2$

We need 2 different z values to solve this equation.

frustum

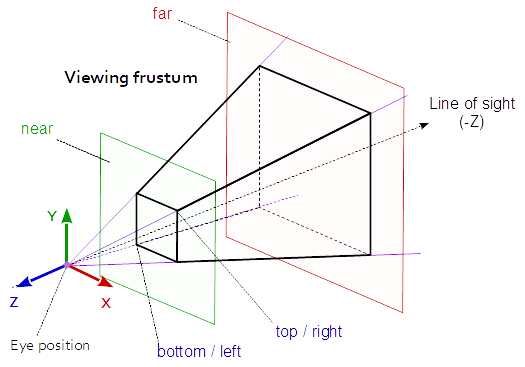
The viewing region(also called frustum) has 2 depth restrictions: near and far. we use n and f to represent these 2 values.
n and f are 2 z values which can be used to solve the equation above.
The solutions of m1 and m2 are:

$m_{1} = n+f$

$m_{2} = nf$

The perspective matrix:

$\begin{bmatrix} n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& -1& 0\\\end{bmatrix}$

Perpective Projection Matrix

After applying perspective transformation and homogeneous divison, the frsutum becomes a axis ligned bounding box.

frustum_to_AABB

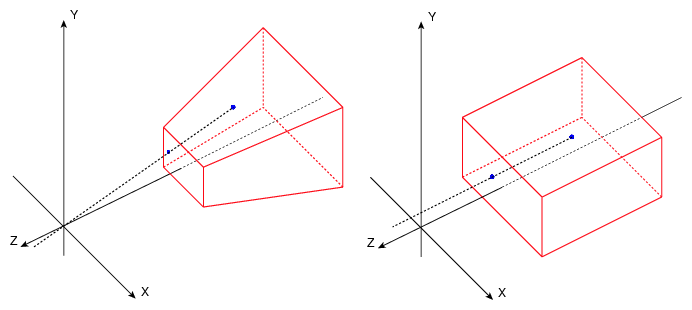
After that, we can apply orthographic projection matrix which transforms the viewing scene(inside AABB) into canonical view volume.

canonical_view

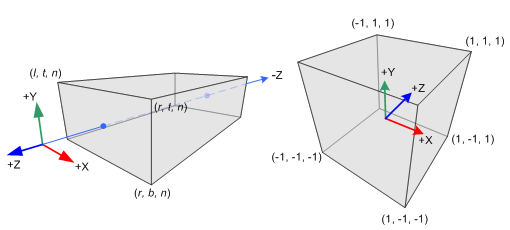
It’s worth mentioning that homogeneous divison is a mutiplication between a scalar(w) and a matrix.

$\frac{1}{w} \begin{bmatrix}M_{p}\end{bmatrix}\begin{bmatrix}x \\ y\\ z\\ w\\\end{bmatrix}$

Homogeneous division can be extracted(scalar factorization), perspective matrix and orthographic projection matrix can be applied first.

$\frac{1}{w}(\begin{bmatrix}M_{ortho}\end{bmatrix} \begin{bmatrix}M_{pers}\end{bmatrix})\begin{bmatrix}x \\ y\\ z\\w\\\end{bmatrix} = \begin{bmatrix}M_{ortho}\end{bmatrix} (\frac{1}{w}\begin{bmatrix}M_{pers}\end{bmatrix} ) \begin{bmatrix} x\\ y\\ z\\w\\\end{bmatrix}$

$\frac{1}{w}(\begin{bmatrix}M_{ortho}\end{bmatrix} \begin{bmatrix}M_{pers}\end{bmatrix})\begin{bmatrix} x\\ y\\ z\\ w\\\end{bmatrix} = \frac{1}{w}(\begin{bmatrix} \frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& -\frac{2}{n-f}& \frac{n+f}{n-f}\\ 0& 0& 0& 1\\\end{bmatrix}\begin{bmatrix} n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& -(n+f)& nf\\ 0& 0& -1& 0\\\end{bmatrix})\begin{bmatrix} x\\ y\\ z\\ w\\\end{bmatrix}$

$\begin{bmatrix} \frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& -\frac{2}{n-f}& \frac{n+f}{n-f}\\ 0& 0& 0& 1\\\end{bmatrix}\begin{bmatrix} n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& -(n+f)& nf\\ 0& 0& -1& 0\\\end{bmatrix}=\begin{bmatrix} \frac{2n}{r-l}& 0& \frac{r+l}{r-l}& 0\\ 0& \frac{2n}{t-b}& \frac{t+b}{t-b}& 0\\ 0& 0& \frac{n+f}{n-f}& \frac{2nf}{n-f}\\ 0& 0& -1& 0\\\end{bmatrix}$

Perpective Projection Matrix:

$\begin{bmatrix} \frac{2n}{r-l}& 0& \frac{r+l}{r-l}& 0\\ 0& \frac{2n}{t-b}& \frac{t+b}{t-b}& 0\\ 0& 0& \frac{n+f}{n-f}& \frac{2nf}{n-f}\\ 0& 0& -1& 0\\\end{bmatrix}$

Credits:
Learn WebGL
OpenGL Projection Matrix by songho
video by Brendan Galea, really good explanation

Perspective Projection

Derivation of Perspective Projection Matrix

Homogeneous Coordinates

Perspective Matrix

Perpective Projection Matrix

FEATURED TAGS

FRIENDS