Orthographic Projection

Orthographic projection projects objects without scaleing objects base on depth.

comparison

The Orthographic projection matrix transfer object inside a scene bounding box into a canonical view volume. Both scene bounding box and canonical view volume are axis aligned.

scene_to_canonical

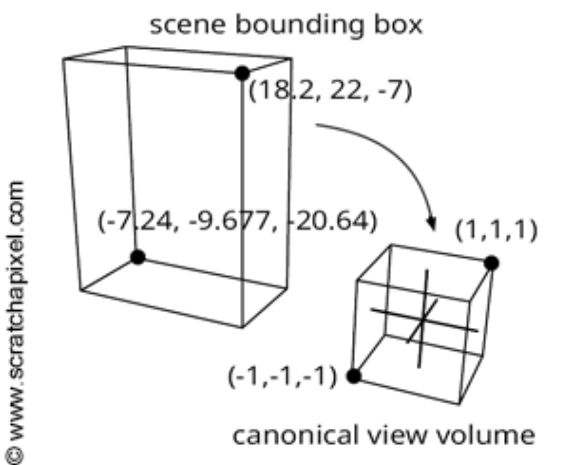
There are some graphic APIs have a range of 0 to 1 for z of the canonical volume. I will stick with -1 to 1 for this derivation.

scene

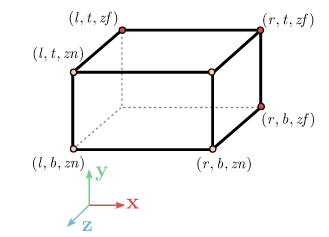
Just like the image above shows, I assume the left bottom near vertex of the scene volume as (l, b, n). And assuming the right top far vertex of the scene volume as (r, t, f).

The idea of the derivation is simple. First, translate the scene volume so that the center of the scene volume coincide with origin. And then I scale the scene volume so that it matchs canonical volume. Last, revert z coordinates.

The center of scene volume is easy to find since (l, b, n) and (r, t, f) are know and the volume is axis aligned. Center of scene volume:

$(\frac{l+r}{2}, \frac{b+t}{2}, \frac{n+f}{2})$

After the translation matrix is applied, the center of view volume should coincide with origin.
Translation matrix:

$\begin{bmatrix} 1& 0& 0& -(\frac{l+r}{2})\\ 0& 1& 0& -(\frac{b+t}{2})\\ 0& 0& 1& -(\frac{n+f}{2})\\ 0& 0& 0& 1\\\end{bmatrix}$

Next, scale the scene volume so that it becomes a cube within the range of [-1, 1].
The length of edges of the scene volume are: r - l, t - b, n - f
Since the length of the edge for canonical volume is 2, so that 2 should be mupltiplied after the division by r - l, t - b, n - f

Scale matrix:

$\begin{bmatrix} \frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& -\frac{2}{n-f}& 0\\ 0& 0& 0& 1\\\end{bmatrix}$

After projection matrix is applied, the z axis should revert. That why there is a negative sign at row 3 column 3

Applying translation matrix first and then scale matrix

$\begin{bmatrix} \frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& -\frac{2}{n-f}& 0\\ 0& 0& 0& 1\\\end{bmatrix}\begin{bmatrix} 1& 0& 0& -(\frac{l+r}{2})\\ 0& 1& 0& -(\frac{b+t}{2})\\ 0& 0& 1& -(\frac{n+f}{2})\\ 0& 0& 0& 1\\\end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1\\\end{bmatrix}$

Matrix has associative property. translation matrix can multiply with scale matrix first which produces the final result.
Orthographic Projection Matrix:

$\begin{bmatrix} \frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& -\frac{2}{n-f}& \frac{n+f}{n-f}\\ 0& 0& 0& 1\\\end{bmatrix}$

Credits:

Scratchapixel 2.0
OpenGL Projection Matrix by songho
video by Brendan Galea, really good explanation
Mathematics for 3D Game Programming and Computer Graphics, Thrid Edition

Orthographic Projection

Derivation of Orthographic Projection Matrix

FEATURED TAGS

FRIENDS