Parametric Lines
Given 2 points, one line can be defined as:
or:
which is as same as:
v is the vector pointing from one point to the other point on the line.
t can be any values, if t is positive, then L(t) represents a ray with a starting point P and a vector v.
Distance Between a Point and a Line
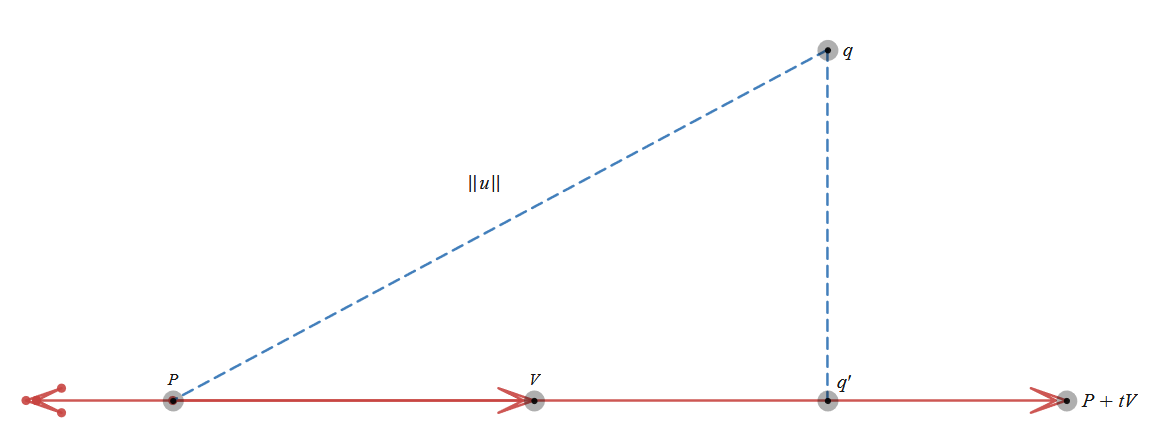
u is the vector from p to q
||u|| is the magnitude of u
We want the shorest distance from point q to line, in the graph above it’s the distance from q to q’.
q’ is the projection of q to the line.
Solution 1
The first solution is intuitive. If the distance pq’ and ||u|| are known, then qq’ can be calculated.
Calculation of ||pq’||
Base on property of dot product:
divided by magnitude of v :
Now ||u|| and ||pq’|| are known, ||qq’|| can be calculated base on Pythagorean theorem.
Problem of this solution
Since positions of point q and p are both unknown so that it’s possible that distance from q to p might be really large. However, this doesn’t necessarily mean point p is far away from the line.
In that case, ||u|| and u dot v may have really large floaing point values. Square of ||u|| and subtracting u dot v will result loss of precesions.
Solution 2
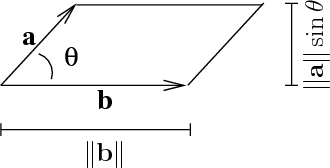
Base on the property of cross product:
The magnitude of a X b is equal to the area of parallelogram with side b and b
The area of parallelogram is also equal to base mupltiply with height.
In our case, base is the magnitude of vector v. Height is ||qq’||
Solution 2 still has substractions between large floating numbers (happens inside cross product), but it’s better because floating point values are not squared first before substraction.
Credits:
Foundations of Game Engine Development, Volume 1 Mathematics
Mathematics for 3D Game Programming and Computer Graphics, Thrid Edition